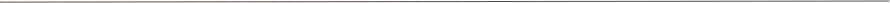
causality or simple correlations

One of the simplest ways of understanding relationships is through looking at the correlation between events.  If some thing always follows another, we can claim that the first causes the second. 

Thus when we kick a ball, it moves, so we can say the kicking the ball causes it to move.  How the ball moves is of course structurally determined; it matters what kind of footwear you kick it with, and it matters what kind of ball it is; and in what condition.  Furthermore the trajectory is dependent on details of just how you kick; so aiming the ball is a matter of expertise.

We all know that the result of an identical kick is different if you kicks a rock, or a snowball that disintegrates, or a dog.  Structural determinism is not violated in the relationship between the response and the action.  It is our ability to distinguish the details of this relationship that enables us to consider it “causal”, that is we can act appropriately according to the structural coherences entailed in the circumstances.

Creative Commons:  
Global Partnership for Education, Honduras

However, not all correlations can be considered causal.  We may look at an indicator of something happening that we do not see, and believe that the indicator causes the next event.  Consider the old rhyme “red sky at night, sailors delight, red sky in the morning, sailors take warning”.   It is not the colour of the sky that determines the possibility of a storm.  Furthermore, the rhyme applies only to certain locations with predictable weather patterns. 

a complex world and causality

If you walk into a room and see a vase toppled over, you might ask “What caused that to happen?”   There could be many different reasons... a person or a pet knocked it over, there was a small tremor from some hammering or machinery, or there was an earthquake... of maybe the flowers were simply arranged in a way that was out of balance.

Going backwards from an event is a different matter than discerning a consistent correlation.  More importantly, what this reveals is that most events can have many different causes, and in a complex system there are usually multiple configurations of causes such that there is no singular thing, say “A” that causes “B”... but rather there has to be a combination such as “A plus K plus S”  or “K plus M plus Y, as long as P is not also happening”. 

The scourge of discerning the interaction between many pollutants, toxic compounds, or circumstances lies in this difficulty.  So, given that most of what matters to us is indeed a complex situation, what can we do?

Every distinction reveals some regularities
in our living and obscures others.

(Maturana, paraphrased)

methods as complex distinctions

I claim that all correlations, and for that matter all methodologies, are grounded in distinctions that are made.  Thus each one that has remained in praxis over time has some utility.  We use methods because they help us see something.  Yet no method serves to show us everything.  If we have multiple methods to look at any situation, we are richer.  If we acknowledge the limitations of any method, we can take greater advantage of the benefits.  I think that the hubris of thinking that any distinction or any methodology, no matter how well articulated, or thorough, is complete or represents “Reality” is dangerous.   Yet I also think that it is equally stupid to throw out all tools because no tool does everything one might wish to do.

correlations between two variables

The word “variable” means just that.  Were not looking at just single events, but things that vary together... eg. increasing one thing may increase the other, or vice versa.  There are a few basic linear relations... i.e. the amount of change in one always has the same relationship to the amount of change in the other, regardless of whether there is a lot or a little of each.   The way to read the graphs representing these relationships is to consider the x axis (the horizontal one) to be the “cause” and the y axis (the vertical one) to be the “effect”. These are known as the independent variable (x axis) and the dependent variable (y axis).  The following graphs do not have axes labels, normally you should indicate the range you are representing for both the independent and dependent variables. 

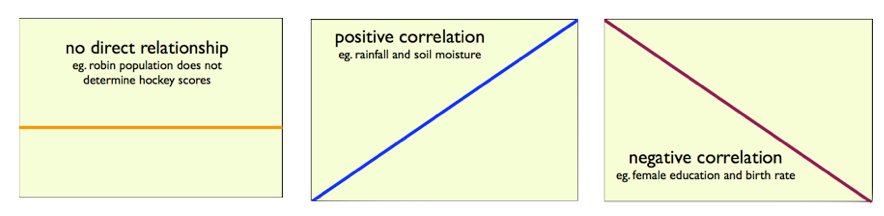
non-linear correlation

Straight lines are not the norm.   There are many other forms of relationship between two variables.  In general if we understand the situation through a deep expertise, we can draw the form.  But that is not also easy due to the many “it depends on” (see multiple influences.) However, there are some patterns, for example something saturates so that the effect becomes less and less as one approaches some maximum value, or the influence of the dependent variable becomes more significant the larger it gets (an exponentially increasing effect.) 

It is of course also have a bimodal influence where it matters at both extremes but not in the middle, or even multimodal.  The more complex it gets, the harder it is to conceptualize the implications.

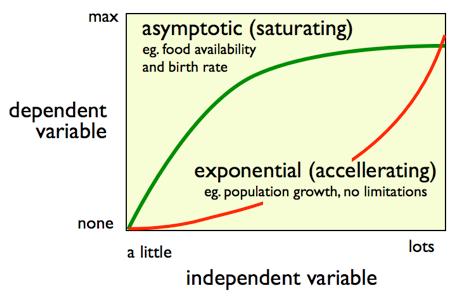
thresholds

the straight lines depicted above are not always the case.  Often the effect of x on y is absorbed for a while, it may be buffered... and then it suddenly exceeds a threshold and we see a rapid change.

There is also often a maximum level beyond which y simply doesn’t change no matter what we do to x. 

Of course thresholds can also apply to a negative correlation, and to non-linear relationships

multiple influences

What if there are several independent variables all influencing the same dependent variable?  Lets say A, B, and C all influence Y.  Do they add up?  Does the influence of A get more or less if B and/or C are present? Do you actually always need C if A is going to have any effect at all? 

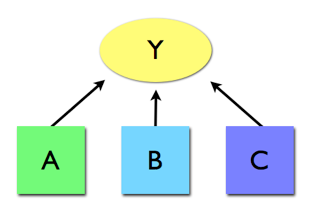
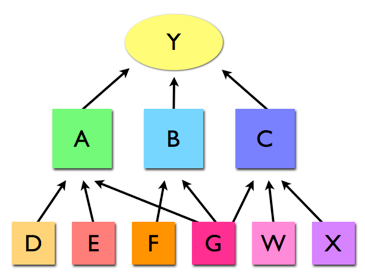
You can imagine further complications and what else might happen if you considered D, E, F, G as well as any number of other influences.  And what if those other influences are one step removed, and invisible to you?   No wonder that we have moved to controlled experiments to discern the influence of any one factor on another... it gets complicated.  However, what we learn from single factor analyses does not tell us of the interactions.

And we have not even considered circular relationships, the “feedback”  influence of Y on X in the simplest case!

S.Kneebone in Ison, Systems Practice